Winter storms had a tremendous impact on Sweden during the first week of January. A low-pressure system named Floriane impacted various parts of north-western Europe.
This example shows analysis of the selected parameters:
zgeopotential at constant pressure level 500 hPa,ttemperature at 850 hPa,mslmean sea level pressure, andtptotal precipitation of the AIFS datasets on 7 January 2025 in Sweden (58.58° N, 11.07° E).
1. Set Up Your Environment and Find ECMWF Open Data¶
Open data will be downloaded from a publicly available Amazon S3 Bucket. First, the following Python libraries need to be installed in the current Jupyter kernel:
ecmwf-opendatato download data andearthkitto analyse and plot the data.
If the packages are not installed yet, uncomment the code below and run it.
# !pip3 install earthkit ecmwf-opendatafrom ecmwf.opendata import Client
import earthkit.data as ekd
import earthkit.plots as ekp
import earthkitList of parameters to retrieve from open datasets¶
The selected values below can be modified.
- Parameters available on pressure levels:
PARAM_PL = "z" # "t"
LEVELS = [500, 850]
LEVELTYPE = "pl"
DATES = [20250104, 20250105, 20250106, 20250107, 20250108]
TIME = 0
STEPS = 0
STREAM = "oper"
TYPE = "fc"
MODEL = "aifs"- Parameters available on a single level:
PARAM_SFC = "tp" # "msl"
LEVELTYPE = "sfc"
DATES = [20250104, 20250105, 20250106, 20250107, 20250108]
TIME = 0
STEPS = 12
STREAM = "oper"
TYPE = "fc"
MODEL = "aifs"Get the data using the ECMWF Open Data API¶
def get_open_data(date, time, step, stream, _type, model, param, leveltype, levelist=[]):
client = Client(source="aws")
list_of_files = []
# Get the data for all dates
for _date in DATES:
filename = f"{model}_{''.join(param)}_{''.join(map(str, levelist))}_{_date}.grib2" if levelist else f"{model}_{''.join(param)}_{leveltype}_{_date}.grib2"
data = client.retrieve(
date=_date,
time=time,
step=step,
stream=stream,
type=_type,
levtype=leveltype,
levelist=levelist,
param=param,
model=model,
target=filename
)
list_of_files.append(filename)
return data, list_of_files2. Temperature at 850 hPa¶
data, list_of_files = get_open_data(date=DATES,
time=TIME,
step=STEPS,
stream=STREAM,
_type=TYPE,
model=MODEL,
param=PARAM_PL,
leveltype=LEVELTYPE,
levelist=LEVELS) # Select AIFS model data from 4 to 8 January 2025
t = ekd.SimpleFieldList()
for _file in list_of_files:
ds = ekd.from_source("file", _file)
md = ds.metadata()
v = ds.to_array()
for f in range(len(md)):
t.append(ekd.ArrayField(v[f], md[f]))
t.ls()Loading...
t850 = t.sel({"level": 850, "shortName": "t"})
t850.head()Loading...
data, list_of_files = get_open_data(date=DATES,
time=TIME,
step=STEPS,
stream=STREAM,
_type=TYPE,
model=MODEL,
param=PARAM_PL,
leveltype=LEVELTYPE,
levelist=LEVELS) Geopotential height is calculated by dividing the geopotential by the Earth’s mean gravitational acceleration, g (=9.80665 m s-2). In the ECMWF Open Charts, it is plotted in geopotential decameters. Therefore, our result also need to be divided by 10.
# Select AIFS model data from 4 to 8 January 2025
z = ekd.SimpleFieldList()
for _file in list_of_files:
ds = ekd.from_source("file", _file)
md = ds.metadata()
v = ds.to_array() / (9.80665 * 10)
for f in range(len(md)):
z.append(ekd.ArrayField(v[f], md[f].override(shortName="gh")))
z.ls()Loading...
gh500 = z.sel({"level": 500, "shortName": "gh"})
gh500.describe("gh")Loading...
data, list_of_files = get_open_data(date=DATES,
time=TIME,
step=STEPS,
stream=STREAM,
_type=TYPE,
model=MODEL,
param=PARAM_SFC,
leveltype=LEVELTYPE,
levelist=[]) A unit of total precipitation is kg/m. 1 kg of rainwater fills an area of 1 m with the water of height 1 mm.
In the ECMWF Open Charts, total precipitation is also plotted in millimetres.
# Select AIFS model data from 4 to 8 January 2025
tp = ekd.SimpleFieldList()
for _file in list_of_files:
ds = ekd.from_source("file", _file)
md = ds.metadata()
v = ds.to_array()
for f in range(len(md)):
tp.append(ekd.ArrayField(v[f], md[f]))
tp.ls()Loading...
data, list_of_files = get_open_data(date=DATES,
time=TIME,
step=STEPS,
stream=STREAM,
_type=TYPE,
model=MODEL,
param=PARAM_SFC,
leveltype=LEVELTYPE,
levelist=[]) We will plot mean sea level pressure data in hPa, therefore we need to divide them by 100.
# Select AIFS model data from 4 to 8 January 2025
msl = ekd.SimpleFieldList()
for _file in list_of_files:
ds = ekd.from_source("file", _file)
md = ds.metadata()
v = ds.to_array() / 100
for f in range(len(md)):
msl.append(ekd.ArrayField(v[f], md[f]))
msl.ls()Loading...
5. Data visualisation¶
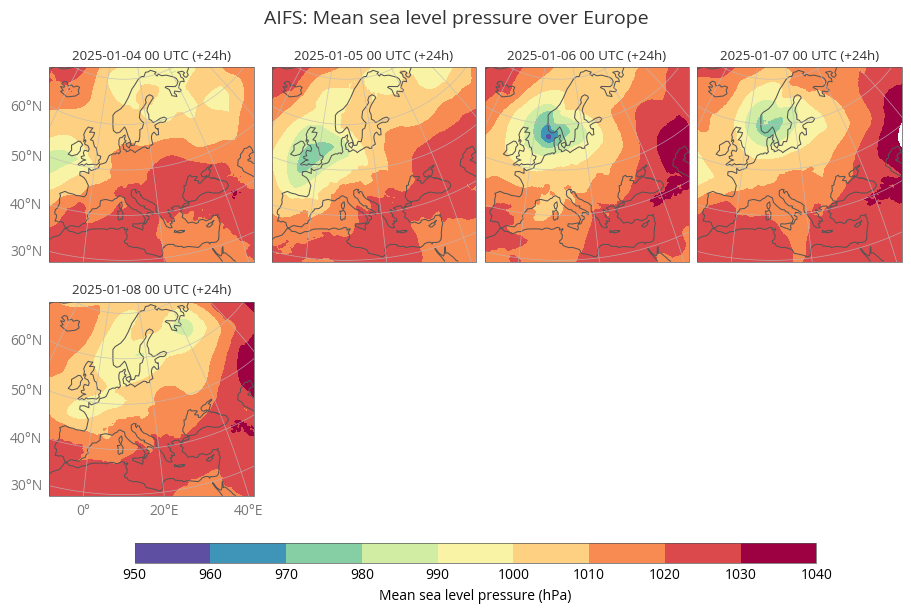
The plots below show analysis of T850 and z500 from 4 to 8 January 2025.
figure = ekp.Figure(domain="Europe", size=(9, 8), rows=3, columns=4)
t850_shade = ekp.styles.Style(
colors="Spectral_r",
levels=range(-40, 50, 2),
units="celsius",
)
for i in range(5):
figure.add_map(1+i//4, i%4)
figure.contourf(t850, style=t850_shade)
figure.coastlines(resolution="low")
figure.gridlines()
figure.legend(location="bottom", label="{variable_name} ({units})")
figure.subplot_titles("{base_time:%Y-%m-%d %H} UTC (+{lead_time}h)")
figure.title(
"AIFS: Temperature at 850 hPa over {domain}\n",
fontsize=14, horizontalalignment="center",
)
figure.save(fname=f"./plots/{PARAM_PL}_{MODEL}_{DATES[-1]}{TIME}-{STEPS}h.png")
figure.show()
figure = ekp.Figure(domain="Europe", size=(9, 8), rows=3, columns=4)
gh500_shade = ekp.styles.Style(
colors="Spectral_r",
levels=range(490, 600, 10),
)
for i in range(5):
figure.add_map(1+i//4, i%4)
figure.contourf(gh500, style=gh500_shade)
figure.coastlines(resolution="low")
figure.gridlines()
figure.legend(location="bottom", label="{variable_name} (gpd)")
figure.subplot_titles("{base_time:%Y-%m-%d %H} UTC (+{lead_time}h)")
figure.title(
"AIFS: Geopotential height at 500 hPa over {domain}\n",
fontsize=14, horizontalalignment="center",
)
figure.save(fname=f"./plots/{PARAM_PL}_{MODEL}_{DATES[-1]}{TIME}-{STEPS}h.png")
figure.show()
The plots below show analysis of total precipitation and mean sea level pressure from 4 to 8 January 2025.
figure = ekp.Figure(domain="Europe", size=(9, 8), rows=3, columns=4)
tp_shade = ekp.styles.Style(
colors="Spectral_r",
levels=range(1, 250, 5),
units="mm",
)
for i in range(5):
figure.add_map(1+i//4, i%4)
figure.contourf(tp, style=tp_shade)
figure.coastlines(resolution="low")
figure.gridlines()
figure.legend(location="bottom", label="{variable_name} ({units})")
figure.subplot_titles("{base_time:%Y-%m-%d %H} UTC (+{lead_time}h)")
figure.title(
"AIFS: {variable_name} over {domain}\n",
fontsize=14, horizontalalignment="center",
)
figure.save(fname=f"./plots/{PARAM_SFC}_{MODEL}_{DATES[-1]}{TIME}-{STEPS}h.png")
figure.show()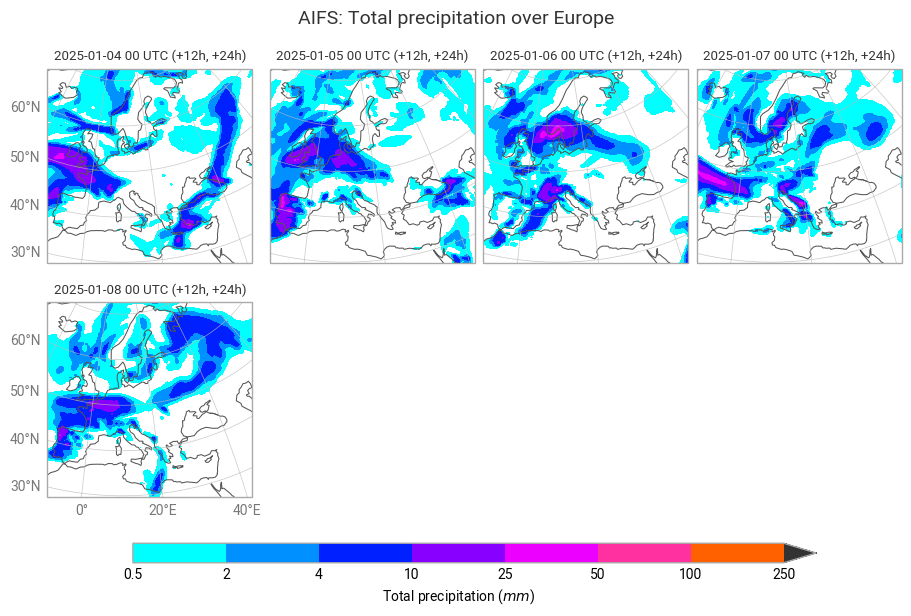
figure = ekp.Figure(domain="Europe", size=(9, 8), rows=3, columns=4)
msl_shade = ekp.styles.Style(
colors="Spectral_r",
levels=range(950, 1050, 10),
)
for i in range(5):
figure.add_map(1+i//4, i%4)
figure.contourf(msl, style=msl_shade)
figure.coastlines(resolution="low")
figure.gridlines()
figure.legend(location="bottom", label="{variable_name} (hPa)")
figure.subplot_titles("{base_time:%Y-%m-%d %H} UTC (+{lead_time}h)")
figure.title(
"AIFS: {variable_name} over {domain}\n",
fontsize=14, horizontalalignment="center",
)
figure.save(fname=f"./plots/{PARAM_SFC}_{MODEL}_{DATES[-1]}{TIME}-{STEPS}h.png")
figure.show()